Examples of application of programs related to nuclear physics
Here are discussed examples of application of programs for calculation of radioactive decay kinetics and similar. For theoretical basis, see the chapter NUCLEAR PHYSICS (in Polish).Example 1
Question:How high would be the activity of a probe of yttrium-90 (Y-90) on 15.07.2012 at 13:30, if it was 1 GBq on 12.07.2012 at 12:00?
Calculations:
1. Calculation of time difference between the time point 1 (12.07.2012, 12:00 - beginning time, date 1), and 2 (15.07.2012, 13:30 - end time, date 2):
For this purpose, you may use the algorithm "Time difference" from "General math options" of the "Calculator". After you launch the program, you have to fill out the form fields with appropriate data. You obtain the following results:
2. Physical half-time of the nuclide Y-90:
The value can be read from this table (Polish), or from another source. Result:
For Y-90 T1/2 = 64.00 h
2. Final calculations:
You have to launch the algorithm "Simple radioactive decay (1 radioactive nuclide: A → B)" in "Calculations related to nuclear physics". In the form fields T1/2(1) (physical half time of the nuclide 1) and t (time elapsed), you have to enter the data expressed in the same units. Because the half time of Y-90 is expressed in hours, the time elapsed must be expressed also in hours; it is equal to 73.5 (see point 1.). So, you have to fill out the form in the following way:
After you click the button "Calculate", you obtain the result:
Nt(1) = 0.45111354195166.
In this algorithm, you can enter the quantity of the nuclide 1 expressed alternatively as either mass (number of atoms, etc.) or activity, because the activity is proportional to the mass (number of atoms, A=λN). Since we assumed in the question that the unit is GBq, the result is expressed in GBq as well. Additionally, we obtain information about the decay constant (λ) and the mean lifetime of the nuclide 1 (τ; nuclide 1 = Y-90), and about the quantity of the products, what arise during this time (nuclide 2 - in our example, it is Zr-90, stable). However, if we consider activity (not mass or number of atoms), the last information should be neglected.
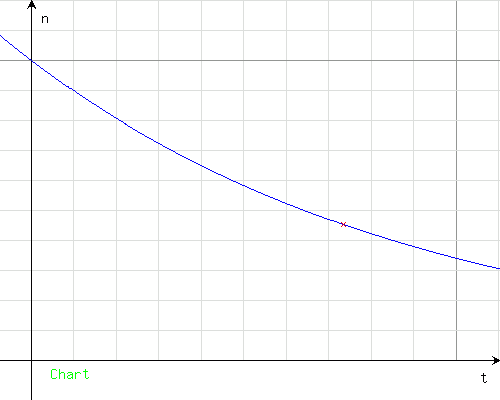
Axis of time (horizontal): 1 unit = 10 hours, 1 bold unit = 100 hours; axis of activity (vertical): 1 unit = 0.1 GBq, 1 bold unit = 1 GBq
Answer:
The activity would be about 0.451 GBq (about 451 MBq).
Example 2
Question:How high would be the activity of a capsule of iodine-131 on 08.07.2012 at 12:00, if its activity for 12.07.2012 at 12:00 (calibration date) was calibrated for 800 MBq?
Calculations:
Our steps are similar as in the example 1. However, because we ask about the time, which is before the time of calibration, you have to enter the time elapsed t in the data preceded with the sign minus (-). So, you have to fill out the form in the following way:
In the result, you obtain the value 1131 (MBq, because the data entered were expressed in MBq).
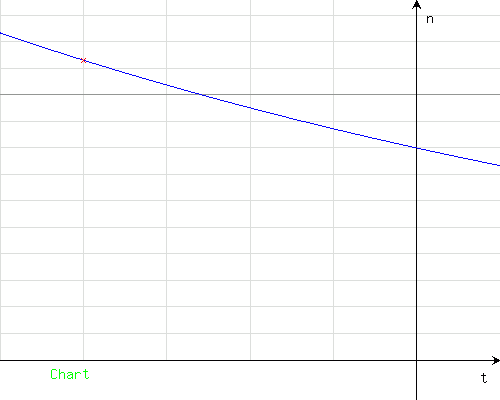
Axis of time (horizontal): 1 unit = 1 day; axis of activity (vertical): 1 unit = 100 MBq, 1 bold unit = 1000 MBq
Answer:
The activity would be about 1131 MBq (about 1.1 GBq)
Example 3
Question:A molybdenum-technetium generator with nominal activity 10 GBq was eluted 5 days after the calibration date. How high would be the activity of technetium-99m in the generator two hours after the elution?
Calculations:
1. After you get the half times of the nuclide 1 (Mo-99, 66 hours) and nuclide 2 (Tc-99m, 6 hours), you should calculate, how much nuclide 1 remains after 5 days. For this purpose, you can use the same algorithm as in the above examples. Because the T1/2(1) is expressed in hours, you should remember to express the time elapsed (t) also in hours (120, not 5). Proceeding according to the algorithm, you get the activity of the nuclide 1 after 5 days equal to 2.8 (GBq).
2. Next, you should launch the algorithm "Successive radioactive decay (2 radioactive nuclides: A → B → C)". In appropriate form fields, you should choose activity (not number of atoms) as the quantity of the nuclide; as the activity of the nuclide 1 at the beginning: 2.8 (remainder of Mo-99 after the elution), as the activity of the nuclide 2 at the beginning: 0 (because the technetium was eluted totally during the elution), the half times of the nuclides 1 and 2: 66 and 6, respectively, branching ratio of the nuclide 1: 87.5 (because only 87.5 % of Mo-99 decays to Tc-99m, the remainder decays directly to Tc-99). Summing up, the form should be filled out in the following way:
In the answer, you get the following numbers (among others):
Quantity of the nuclides after the time t:
At(1) = 2.7418008722888
At(2) = 0.49996042205082
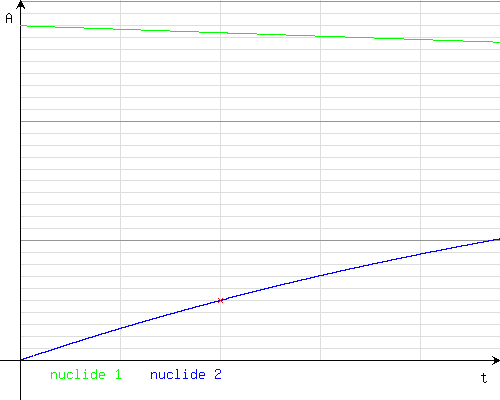
Axis of time (horizontal): 1 unit = 1 hour; axis of activity (vertical): 1 unit = 0.1 GBq, 1 bold unit = 1 GBq
Answer:
The activity of technetium-99m would be about 0.5 GBq (about 500 MBq).