




Średnica atomu jest rzędu nanometra (miliardowa część metra). Prawie cała masa atomu umieszczona jest w małym jądrze. Wokół jądra krążą elektrony, położone na różnych stanach energetycznych ("na różnych orbitach"). Elektrony mają ładunek ujemny. Jądro składa się z nukleonów: naładowanych dodatnio protonów oraz elektrycznie obojętnych neutronów; masa nukleonu jest około dwóch tysięcy razy wyższa od masy elektronu.
Celem opisania jądra określamy je liczbą atomową równą ilości zawartych w nim protonów (której odpowiada określony symbol pierwiastka w układzie okresowym) oraz liczbą masową (ilość nukleonów w jądrze). Liczba masowa odpowiada tylko w przybliżeniu masie atomowej (ze względu na energię wiązania). Liczby te umieszczamy w indeksach przed symbolem pierwiastka. Na przykład symbol 43Tc oznacza atom technetu (który posiada liczbę atomową równą 43), zaś symbol 53I oznacza atom jodu (liczba atomowa 53). Symbol 127I oznacza atom jodu, którego jądro posiada 127 nukleonów: 53 protony (bo taka jest liczba atomowa jodu) oraz 127-53=74 neutrony (jest to jedyny trwały izotop jodu). Symbol 99mTc oznacza izotop technetu (liczba atomowa 43) o liczbie masowej 99, znajdujący się w stanie metastabilnym (znaczenie - patrz dalej). Ostatnie dwa atomy możemy opisać jako I-127 oraz Tc-99m. "Kompletne" symbole powyższych nuklidów są następujące:
| 127 53 | I |
| 99m 43 | Tc |
Atomy, których jądra zawierają tę samą ilość protonów, ale inną ilość neutronów, nazywamy izotopami; należą one do tego samego pierwiastka chemicznego (mają te same właściwości chemiczne). Jądra o tej samej liczbie neutronów to izotony, zaś o tej samej liczbie masowej - izobary. Zbiór atomów o tej samej liczbie protonów i neutronów nazywamy nuklidem.
Zarówno elektrony na powłokach elektronowych jak i nukleony w jądrze atomowym mogą pozostawać w stanie równowagi (atomy trwałe lub stabilne), albo posiadać nadmiar energii, który musi zostać usunięty w postaci promieniowania. Atomy nietrwałe (niestabilne) możemy dalej podzielić na atomy znajdujące się w stanie wzbudzonym (które muszą pozbyć się nadmiaru energii natychmiast - w czasie rzędu ps lub szybciej) oraz w stanie metastabilnym (mogące oddać ten nadmiar z opóźnieniem).
Jądro atomowe, lub atom jako całość, nie będące w stanie równowagi musi wypromieniować nadmiar energii -
Rozpad alfa (oznaczany α) to wypromieniowanie z jądra tak zwanej cząstki alfa (α), czyli jądra atomu helu-4 (składającego się z 2 protonów i 2 neutronów). Jądro potomne (powstające w wyniku takiego rozpadu) jest
| 222 88 | Ra | → | 218 86 | Rn + | 4 2 | He | (6,7 MeV) |
Rozpad beta minus (oznaczany β-) to emisja elektronu (negatonu) oraz antyneutrina elektronowego. W wyniku tego rozpadu powstaje jądro o tej samej liczbie masowej oraz o liczbie atomowej o jeden wyższej. Zachodzi w przypadku jąder o nadmiarze neutronów w stosunku do protonów. Energia rozpadu β- wynosi od niewielu keV do kilku MeV
Przykład rozpadu β-:
| 90 39 | Y | → | 90 40 | Zr | + | e- | + | antyneutrino |
Rozpad beta plus (oznaczany β+) to emisja pozytonu (czyli elektronu o dodatnim ładunku elektrycznym, będącego antycząstką negatonu) i neutrina elektronowego. Energia emitowanych cząstek jest dzielona pomiędzy nie podobnie, jak w przypadku rozpadu β-. Ten rodzaj rozpadu jest typowy dla jąder lekkich, o nadmiernej w stosunku do neutronów ilości protonów. W jego wyniku powstaje atom o tej samej liczbie masowej i o liczbie atomowej o jeden niższej.
Przykład rozpadu β+:| 18 9 | F | → | 18 8 | O | + | e+ | + | neutrino |
Wychwyt elektronu (ang.: electron capture, skrót: EC, oznaczany też ε) polega na przechwyceniu jednego z elektronów (z powłok elektronowych) przez jądro. W efekcie jeden
| 68 32 | Ge | → | 68 31 | Ga | + | neutrino |
Rozszczepieniem (ang.: fission) nazywamy "pęknięcie" jądra na dwie, rzadziej trzy lub więcej, nierówne części. Najczęściej towarzyszy mu emisja kilku neutronów. Dotyczy w zasadzie tylko jąder najcięższych (transuranowce, czyli sztucznie wytworzone pierwiastki cięższe od uranu), u których bywa główną drogą rozpadu (np.: Fm-256 - 92 %, Cf-254 - 99,7 %). Nieco rzadziej ma miejsce jednak także u nuklidów występujących naturalnie (np.: U-238 - 5,45·10-5 %).
POWRÓT do początku podstronyRozpad klastrowy, nazywany też "rozpadem egzotycznym" lub "promieniotwórczością ciężkojonową" (ang.: cluster emission, cluster decay) to bardzo rzadko spotykany rodzaj emisji "klastra", czyli jądra cięższego od cząstki α. Mogą to być jądra 12C, 14C, 20O, a nawet jądra neonu, magnezu i krzemu. Emisja clustera zachodzi w przypadkach jąder niektórych izotopów pierwiastków ciężkich typu rad, frans, aktyn, protaktyn, tor, uran i transuranowce. Te pierwiastki rozpadają się zazwyczaj poprzez emisję cząstek alfa, emisja klastera jest rzadką alternatywą (od 10-5 do 10-16).
Przykład emisji klastera:| 222 88 | Ra | → | 208 82 | Pb + | 14 6 | C | (energia: 30,97 MeV, częstość: ok. 3,7*10-8%) |
Opóźniona emisja neutronu, protonu lub innych cząstek - dotyczy jąder o bardzo dużej dysproporcji ilości neutronów i protonów. Zachodzi prawie natychmiast po innym rodzaju rozpadu (np. beta lub rozszczepienie).
POWRÓT do początku podstronyJest to wyemitowanie przez jądro nadmiaru energii w postaci kwantu promieniowana elektromagnetycznego gamma (oznaczanego γ). Może towarzyszyć innemu rodzajowi rozpadu (np. β-, jak w przypadku kobaltu-60) i zachodzić prawie natychmiast po tym rozpadzie, może też istnieć jako samodzielny rozpad w przypadku tak zwanych jąder metastabilnych, na przykład Tc-99m. Wówczas emisja ta nosi nazwę "przejście izomeryczne" (ang.: isomeric transition, skrót: IT). Energia takiego rozpadu zawiera się zwykle w przedziale od kilkudziesięciu keV do kilku MeV.

| 60 27 | Co | → | 60 28 | Ni | + | e- | + | antyneutrino | + | γ | (1,17, 1,33 MeV) |
| 99m 43 | Tc | → | 99 43 | Tc + | γ | (142 keV) |
Emisja ta polega również na wyemitowaniu nadmiaru energii z jądra. Różnicą jest, że energia ta zostaje przekazana jednemu z elektronów krążących wokół jądra. Elektron ten zostaje wyrzucony z atomu. Jego energia kinetyczna jest,
Oczywistym warunkiem umożliwiającym zajście tego procesu jest to, że energia wiązania elektronu (czyli energia potrzebna do jego oderwania od macierzystego atomu) musi być niższa od energii emitowanego przez jądro kwantu γ. Energia kinetyczna elektronu konwersji jest różnicą między energią wiązania tego elektronu a energią emitowanego przez jądro kwantu gamma.
Emisja elektronu konwersji, ze względu na podobieństwo do zjawiska fotoelektrycznego, bywa nazywana "efektem fotoelektrycznym wewnętrznym". Zasadnicza różnica pomiędzy tymi dwoma procesami polega na tym, że w przypadku elektronu konwersji energia zostaje przekazana elektronowi z tego samego atomu. Inną nazwą tego procesu jest "konwersja wewnętrzna" (ang.: internal conversion, skrót: IC).

Jest to emisja kwantu promieniowania elektromagnetycznego spowodowana przechodzeniem elektronu z wyższego
Proces ten jest nieco różny od wytwarzania promieniowania X w aparatach rentgenowskich. W lampie rentgenowskiej rozpędzone do wysokich energii (prędkości) elektrony zostają wyhamowane podczas przelatywania w pobliżu jąder metalu ciężkiego (zazwyczaj wolfram); towarzyszy temu emisja promieniowania hamowania ("bremsstrahlung"), którego fotony mają bardzo różną energię (widmo ciągłe). Czasami elektron taki wybija elektrony z powłok elektronowych tego atomu - wówczas następuje dodatkowo typowa opisana powyżej emisja charakterystycznego promieniowania X.

| 201 81 | Tl | → | 201 80 | Hg* | + | neutrino |
| 201 80 | Hg* | → | 201 80 | Hg | + | X | (~70-80 keV) |
Jest to proces spowodowany przez te same przyczyny, jak emisja promieniowania X. Różnicą jest, że energia, zamiast zostać wypromieniowana w postaci promieniowania elektromagnetycznego, zostaje przez elektron zmieniający swój stan energetyczny przekazana innemu elektronowi. Wskutek tego powstaje atom, któremu na jednej z powłok brakuje dwóch elektronów. Niektóre atomy, jak na przykład I-125, mogą emitować podczas rozpadu nawet około 20 elektronów Augera.

Wiele nuklidów może podlegać rozpadowi na kilka sposobów. Miarą udziału określonej drogi rozpadu w danym nuklidzie (czyli "częstości rozpadu") jest t.zw. "współczynnik podziału" lub "współczynnik rozgałęzienia" (ang.: branching ratio). Na przykład miedź-64 może rozpadać się na trzy sposoby: poprzez wychwyt elektronu, rozpad β- oraz rozpad β+. Współczynniki podziałów dla tych sposobów rozpadu Cu-64 wynoszą: 43 % dla EC, 39 % dla β- oraz 18 % dla β+.
POWRÓT do początku podstronyOddziaływanie promieniowania z materią jest odpowiedzialne za ewentualne skutki szkodliwe i/lub lecznicze promieniowania, a także umożliwia jego wykrycie. Oddziaływanie to jest zależne od masy, energii kinetycznej i ładunku elektrycznego cząstek, a w przypadku promieniowania elektromagnetycznego od energii kwantów.
POWRÓT do początku podstrony
Oddziaływanie cząstek ciężkich naładowanych (np. protony, cząstki alfa, fragmenty po rozszczepieniu) jest zależne
Oddziaływanie elektronów (cząstek beta) jest także zależne od ich energii, ale efekt Bragga jest słabiej wyrażony, niż w przypadku cząstek o dużej masie. Pierwszy mechanizm wytracania energii jest również związany z jonizacją, czyli "odrywaniem" elektronów od atomów ośrodka, w którym zachodzi wyhamowywanie. Jeżeli elektrony powstające
Droga elektronu jest, ze względu na małą masę, podobna do szybkiej piłeczki ping-pongowej odbijającej się
Oddziaływanie antycząstek (np. pozytonów) polega na anihilacji po spotkaniu z odpowiednią cząstką: para cząstka-antycząstka po prostu "znika" pozostawiając po sobie energię. W przypadku pary negaton-pozyton są to najczęściej dwa fotony o energiach ok. 511 keV (energia spoczynkowa elektronu, wynikająca z prostego przeliczenia masy
Oddziaływanie fotonów z materią odbywać się może w pięciu mechanizmach: rozpraszanie Rayleigh'a, efekt Comptona, efekt fotoelektryczny, tworzenie par negaton-pozyton oraz wywoływanie reakcji nuklearnych. Pierwsza
Oddziaływanie neutronów podlega nieco bardziej skomplikowanym regułom. Jako cząstki pozbawione ładunku elektrycznego nie powodują bezpośredniej jonizacji materii. Wytracanie energii następuje początkowo wskutek zderzania z jądrami atomów ośrodka. Zderzenia te mogą być elastyczne lub nieelastyczne. Podczas zderzeń elastycznych energia kinetyczna neutronu zostaje rozdzielona między neutron a jądro, z którym on się zderzył (przekazanie części energii jądru); w wyniku tego neutron traci część energii, a "trafione" jądro zostaje odrzucone (cząsteczka, w skład której wchodzi, zostaje zniszczona, a samo jądro staje się dodatnim jonem o wysokiej energii, zdolnym do jonizacji). Podczas zderzenia nieelastycznego część energii kinetycznej zostaje zamieniona na kwant gamma.
Swobodny neutron, po wytraceniu części energii kinetycznej, najczęściej łączy się z jakimś jądrem wyzwalając jakąś reakcję jądrową.
Do najczęściej wykorzystywanych w praktyce reakcji z udziałem neutronów należy tak zwana "aktywacja" atomów. Jądra wielu atomów mają zdolność pochłaniania neutronu, czemu zazwyczaj towarzyszy emisja kwantu γ - są to tak zwane "reakcje (n,γ)". W ten sposób produkowane są liczne radionuklidy (jak np. Co-60) dla zastosowań przemysłowych czy medycznych. Dość szczególne miejsce zajmuje reakcja rozszczepienia jądra atomowego pod wpływem neutronu. Polega ona na "pęknięciu" jądra na dwie, rzadziej trzy lub więcej, nierówne części i wyzwoleniu ogromnej energii (około 200 MeV). Reakcji tej ulegają niektóre jądra ciężkie (najważniejsze przykłady: U-235 i Pu-239). Ponieważ procesowi temu towarzyszy emisja kilku neutronów, może on się "sam napędzać", jeśli przekroczona została t.zw. "masa krytyczna". Proces wykorzystywany jest w reaktorze jądrowym oraz w bombie atomowej. Dosyć ciekawą reakcją jest "pękanie" niektórych lżejszych jąder pod wpływem neutronów, czemu nie towarzyszy emisja neutronów. Przykładem jest jądro boru-10. Powstałe w tym procesie fragmenty (jądro helu-4, czyli cząstka α, oraz jądro litu-7) posiadają ogromną energię, dzięki czemu potencjalnie mogą być wykorzystywane do terapii (BNCT - boron neutron capture therapy).
Miarą prawdopodobieństwa zajścia reakcji jądrowej pod wpływem cząstek (m.in. neutronów) jest t.zw. "przekrój czynny". Wielkość ta jest różna dla różnych wartości energii neutronu.
POWRÓT do początku podstrony
Działanie biologiczne promieniowania jonizującego posiada trzy fazy. Najpierw dochodzi do reakcji fizycznych (powyżej opisanych) - to trwa bardzo krótko. Potem następuje faza chemiczna - przekształcenie lub rozpad związków chemicznych znajdujących się w pobliżu miejsc, gdzie energia była przekazywana. Ta faza trwa zazwyczaj
Dawki promieniowania jonizującego mierzymy w zależności od tego, jaka energia (fizycznie) zostanie przekazana ośrodkowi (na przykład organizmowi) lub od tego, jaki efekt biologiczny ta energia spowoduje (tylko organizmy żywe). Dawką fizyczną (ekspozycyjną) jest grej (1 Gy), który odpowiada przekazaniu energii jonizacyjnej równej jednemu dżulowi ośrodkowi o masie jednego kilograma [1Gy=1J/1kg]. Według starych jednostek 1 Gy był równy 100 radom (rad - Radiation Absorbed Dose). Jednostką dawki biologicznej (pochłoniętej, zaabsorbowanej) jest sievert (1 Sv), starą jednostką jest rem (Rentgen Equivalent Man, 1Sv=100rem). Aby przeliczyć greje na sieverty należy przemnożyć dawkę ekspozycyjną (greje) przez tak zwany "współczynnik jakości promieniowania" Q, który jest zależny od rodzaju promieniowania i jego energii. Przykładowo dla elektronów i kwantów gamma wynosi on około 1, dla cząstek alfa około 20, dla neutronów (w zależności od energii) od kilku do około 20. Tak duża rozpiętość tego współczynnika wynika w głównej mierze z różnej gęstości jonizacji: cząstki o dużej gęstości jonizacji mają wysoki współczynnik Q,
W fizyce oraz w medycynie nuklearnej nie jest ważne, jaką masę dana substancja czy też dany lek posiada, tylko jaką energię ze sobą niesie. Miarą ilości substancji promieniotwórczej jest zatem ilość rozpadów radioaktywnych danej próbki na sekundę. Jeden rozpad na sekundę to aktywność równa 1 Bq (bekerel - od nazwiska Antoine Henri Becquerel'a - laureata nagrody Nobla wspólnie z M. Skłodowską i jej mężem w 1903 roku). Starszą jednostką jest Kiur (Ci, od nazwiska M. Skłodowskiej-Curie), którego definicja mówi, że jest to aktywność (ilość rozpadów radioaktywnych na sekundę) równa aktywności 1 grama czystego radu-226 (przy czym 1 Ci = 3,7·1010Bq). Jako ciekawostkę można nadmienić, że próbka jodu-131 o aktywności 1 GBq (czyli 1 miliarda rozpadów na sekundę -
Na jednej z naszych podstron można przeliczać jednostki aktywności (tradycyjne na nowe i na odwrót), a także aktywność substancji promieniotwórczej na jej masę (i na odwrót).
|
Moc dawki (natężenie promieniowania) gamma jest wprost proporcjonalna do aktywności źródła promieniotwórczego oraz do stałej charakterystycznej dla danego nuklidu. Jest ona także odwrotnie proporcjonalna do kwadratu odległości od źródła (efekt pochłaniania promieniowania w ośrodku pominięto). Oznacza to, że dwukrotne zwiększenie odległości od źródła promieniotwórczego zmniejsza natężenie promieniowania γ czterokrotnie. Dla promieniowań innego rodzaju zależności te w próżni są zachowane, w ośrodkach innych jednak mają one bardziej złożony charakter.
Rozpad promieniotwórczy zachodzi zgodnie z równaniem:
N(t)=N(0)e-λt (jest to równanie rozpadu),
gdzie:
- t - czas,
- N(t) - ilość atomów nuklidu po upływie czasu t,
- N(0) - ilość początkowa atomów nuklidu,
- λ - stała rozpadu, charakteryzująca szybkość rozpadu danego nuklidu; 1/λ=T(ż) ("czas życia"), czyli czas, po którym dana próbka nuklidu mogłaby się rozpaść, gdyby proces rozpadu miał do końca stałą prędkość.
Aktywność (A) danej substancji promieniotwórczej jest proporcjonalna do ilości jej atomów: A=λN, więc równanie powyższe może mieć postać:
A(t)=A(0)e-λt.
Ponieważ istnieje prosta zależność pomiędzy t.zw. czasem połowicznego zaniku (T(1/2) - patrz dalej) a λ: T(1/2)λ=ln2, więc równanie rozpadu może przyjąć następującą postać:
N(t)=N(0)2-t/T(1/2).
Wielkość T(1/2) jest charakterystycznym dla każdego nuklidu tak zwanym czasem połowicznego zaniku, czyli czasem,
1/T(1/2)ef = 1/T(1/2)fiz + 1/T(1/2)biol .
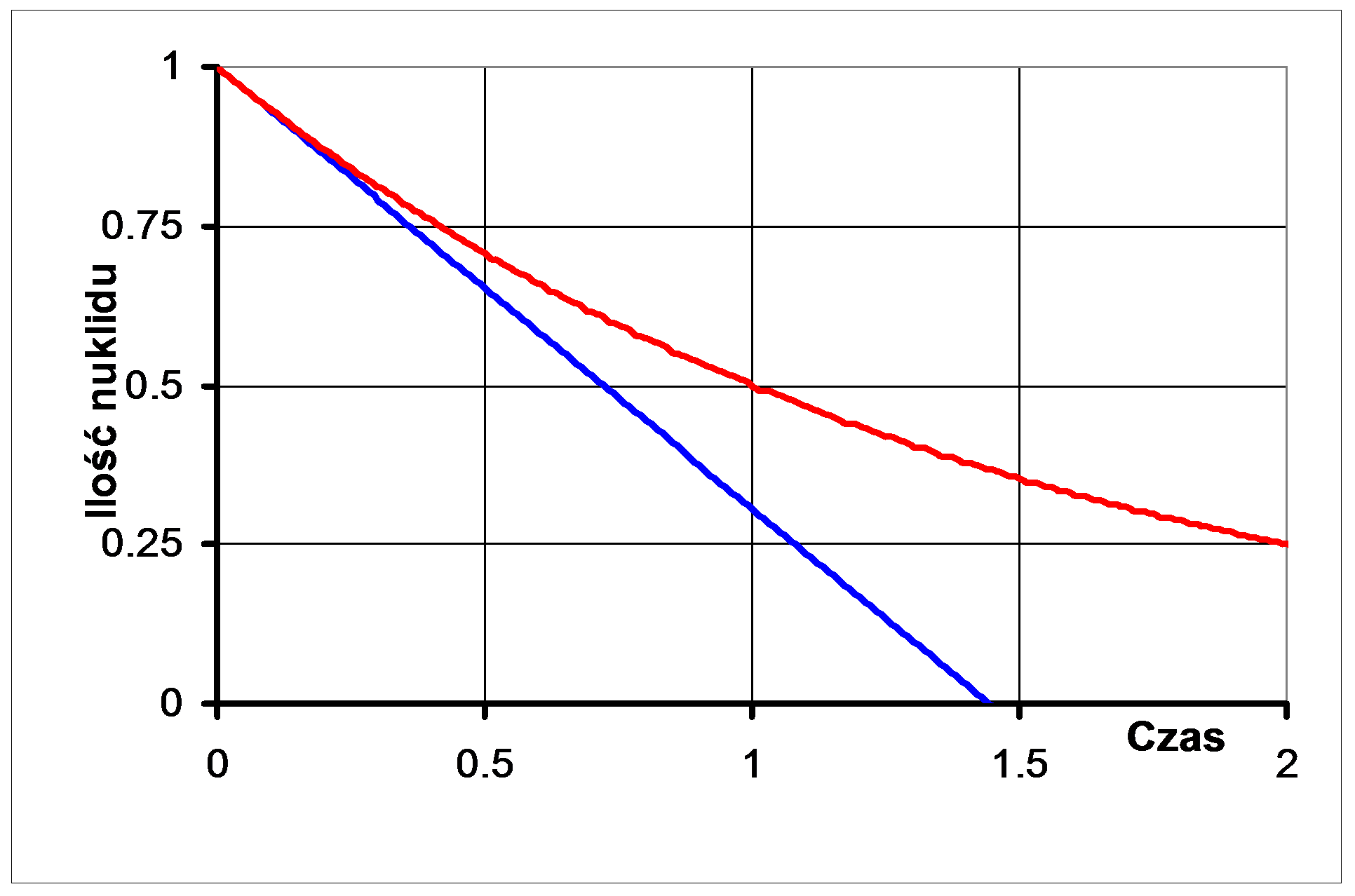
Na podstronie poświęconej różnym obliczeniom znajduje się również opcja obliczania ilości nuklidu
Jeżeli nuklid potomny powstający w wyniku rozpadu nuklidu macierzystego jest także promieniotwórczy, to jego ilość w funkcji czasu można wyliczyć na podstawie tak zwanych równań Batemana. Przykładowe rozwinięcie równania dla ilości atomów drugiego nuklidu radioaktywnego powstającego w wyniku rozpadu nuklidu pierwszego (przy ilości początkowej nuklidu 2 równej zero) wygląda następująco:
 ,
, ,
,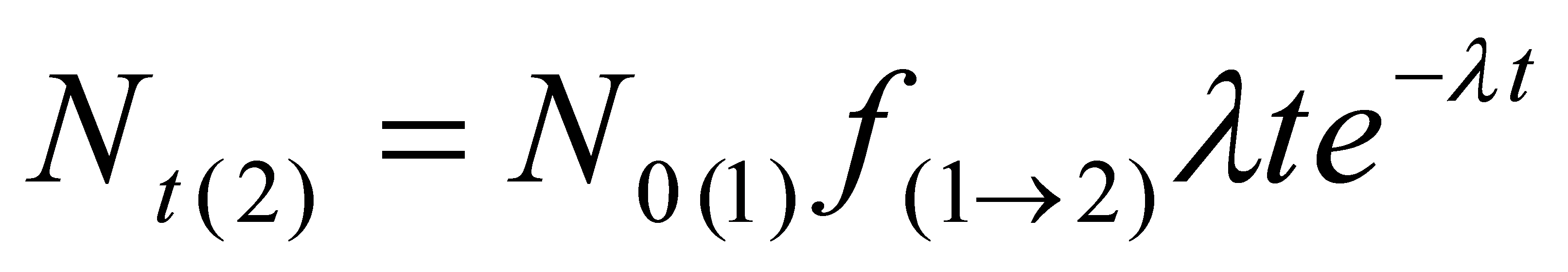 ,
,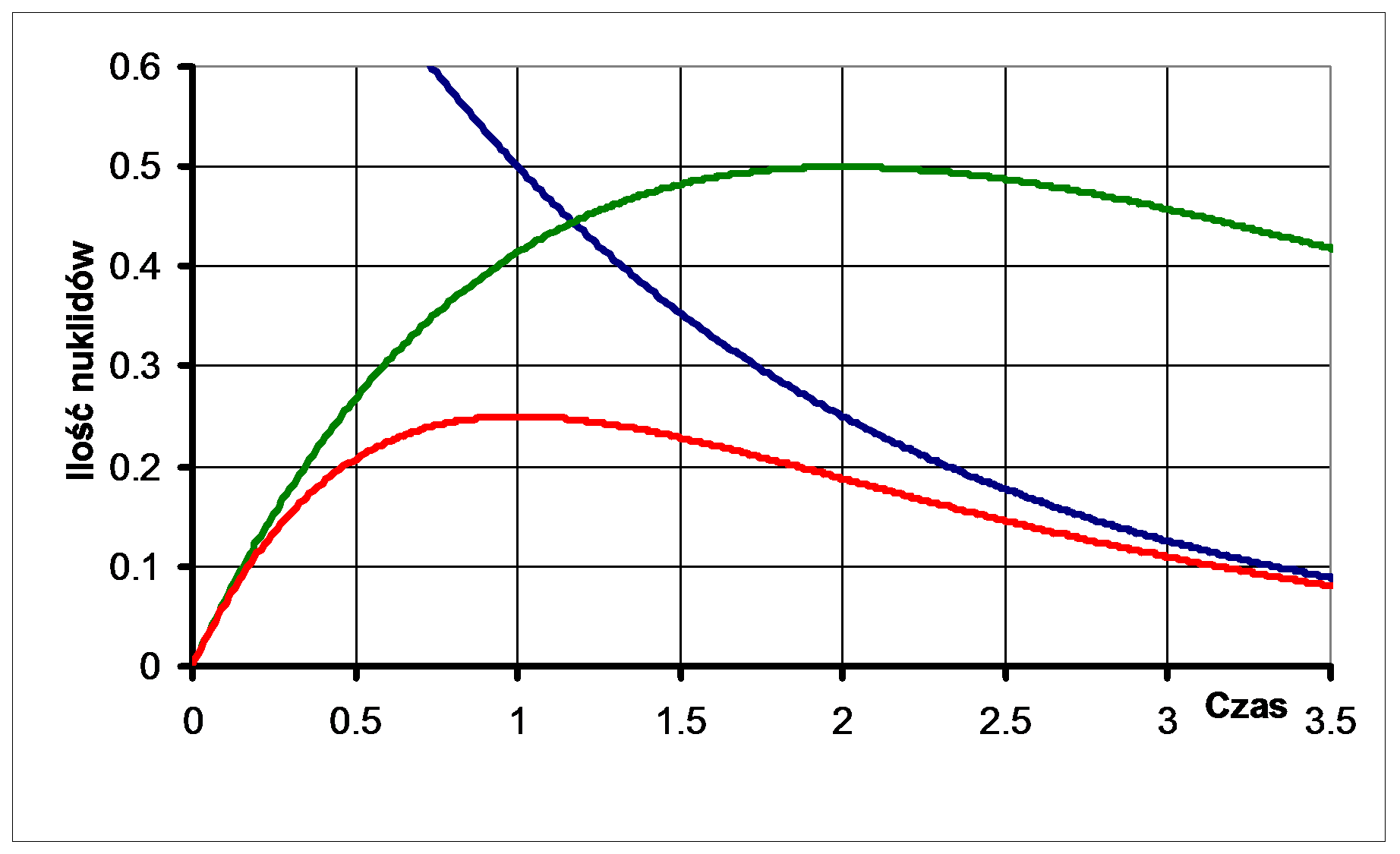
Ciekawa sytuacja następuje, gdy czas połowicznego zaniku nuklidu potomnego jest wyraźnie krótszy od czasu nuklidu macierzystego (czyli λ2>λ1) przy współczynniku podziału równym 1. Wówczas, po pewnym czasie, ustala się stan równowagi: stosunek ilości atomów nuklidów A i B jest zbliżony do stosunku ich stałych rozpadów:
NA/NB ≈ λ2/λ1,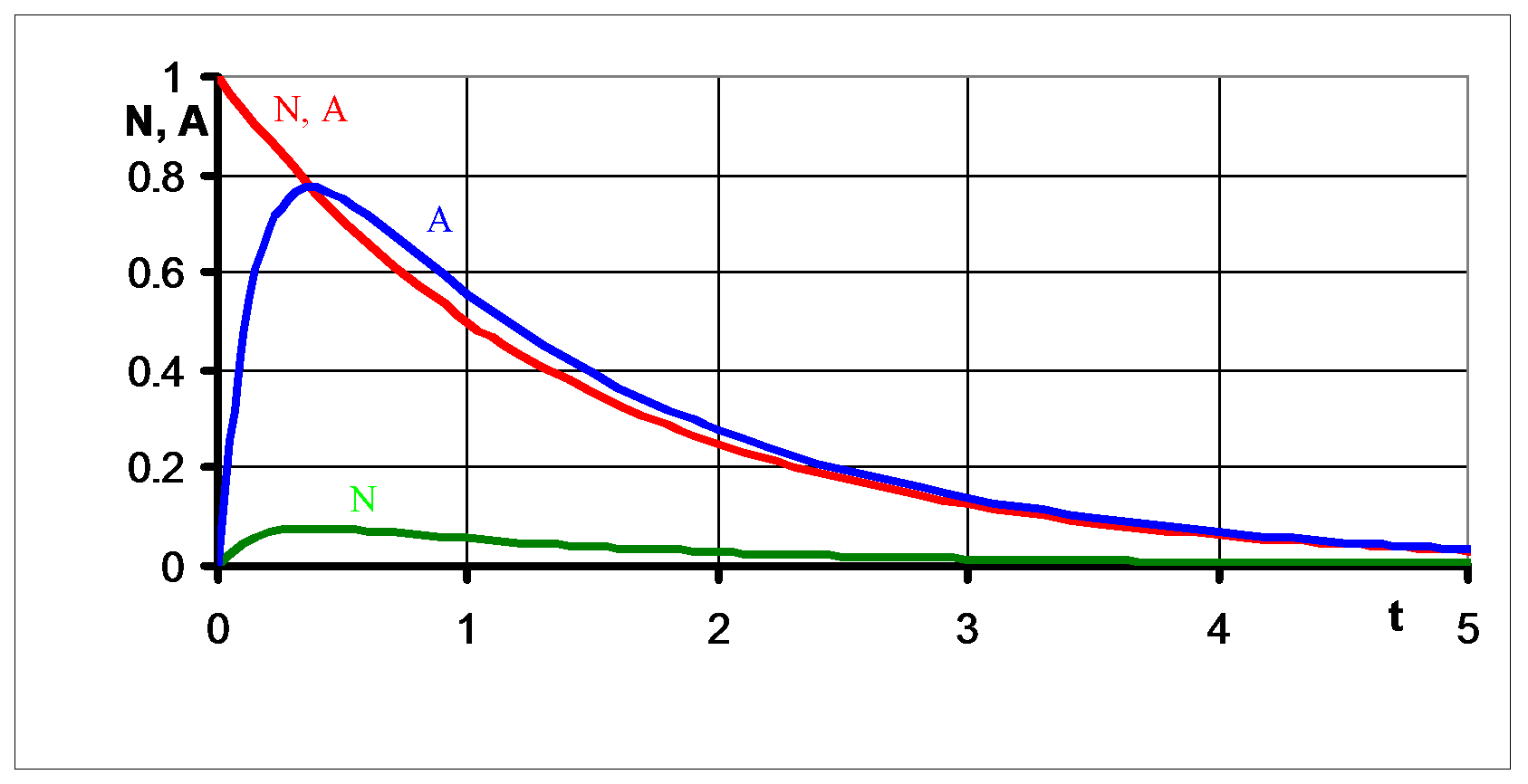
Rozwinięcie równania Batemana dla ilości atomów trzeciego nuklidu w szeregu (przy początkowej ilości atomów nuklidu 2 i 3 równych 0, dla współczynników podziałów nuklidów 1 i 2 równych 1) wygląda jeszcze bardziej skomplikowanie:
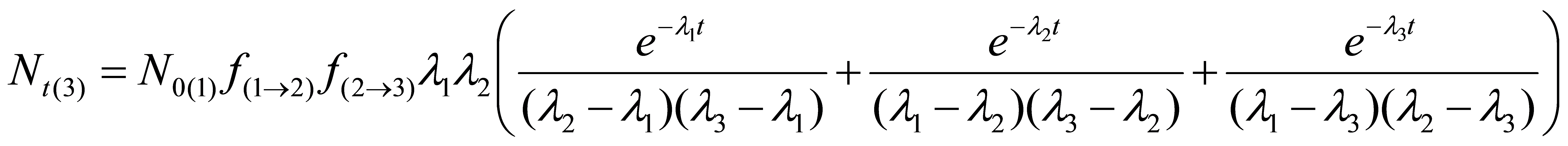
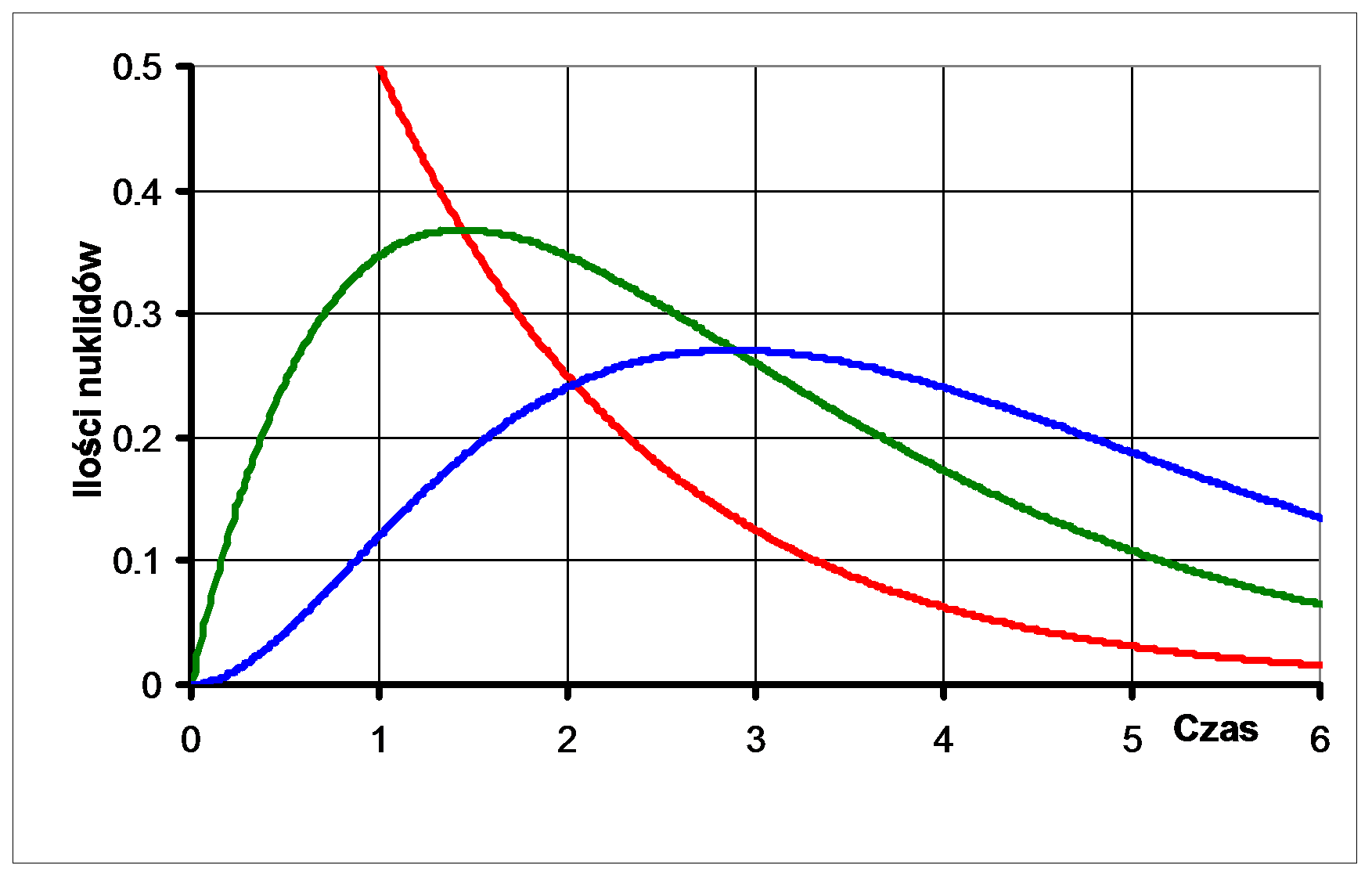
Na podstronie poświęconej różnym wyliczeniom znajduje się również opcja obliczania ilości i aktywności pierwszego nuklidu potomnego o podanym czasie połowicznego zaniku powstającego po rozpadzie nuklidu macierzystego - również o podanym czasie połowicznego zaniku - po upływie określonego czasu. Do obliczeń zostanie dynamicznie wygenerowany wykres. Podobnie można obliczyć ilość kolejnego nuklidu potomnego.
Dozymetrią nazywamy dział fizyki jądrowej zajmujący się przede wszystkim pomiarem i obliczaniem dawek promieniowania jonizującego - głównie w odniesieniu do organizmów żywych. Z praktycznego punktu widzenia możemy podzielić ją na dozymetrię promieniowania o dalekim zasięgu (promieniowanie γ, X, neutrony) oraz o krótkim zasięgu (cząstki α, β it.p.). W medycynie najczęstsze zastosowanie lecznicze znajdują źródła promieniowania o dalekim zasięgu (głównie γ i X) umieszczone poza ciałem pacjenta (radioterapia, teleradioterapia) lub jako źródło zamknięte umieszczone wewnątrz ciała (w pobliżu np. guza - brachyterapia), a także otwarte źródła promieniotwórcze - substancje znakowane radionuklidami emitującymi promieniowanie o krótkim zasięgu (α i β). Te ostatnie są przedmiotem zainteresowania medycyny nuklearnej, zostają podane pacjentowi (doustnie lub wstrzyknięte) i same dzięki swoim właściwościom chemicznym i farmakologicznym muszą dotrzeć do tkanek docelowych - tak, jak "tradycyjne" leki. Podobnie podawane są γ-emitery w celach diagnostycznych, ale dawka promieniowania pochłoniętego jest w przypadku ich zastosowania niewielka.
Nietrudno zauważyć, że dawka promieniowania o krótkim zasięgu jest zależna nie tylko od właściwości fizycznych radionuklidu, ale także od właściwości chemicznych/farmakologicznych radiofarmaceutyku ("nośnika", na którym znajduje się radionuklid). Znalezienie takowej (możliwej do połączenia z odpowiednim radioizotopem) substancji, która gromadziłaby się selektywnie na przykład w tkance nowotworowej, a nie w tkankach zdrowych, umożliwiłoby dostarczenie wysokich dawek promieniowania komórkom guza przy jednoczesnym oszczędzeniu narządów zdrowych. W przypadku wielu schorzeń cel ten już udało się osiągnąć.
Na podstronie poświęconej różnym wyliczeniom znajduje się również opcja obliczania dawki promieniowania o krótkim zasięgu w tkankach.
Rejestracja fotonów promieniowania γ (gamma) oraz X (rentgenowskich) - czyli promieniowania o długim zasięgu - jest oczywiście niemożliwa za pomocą zwykłych technik optycznych; fotony te są przecież niewidoczne dla ludzkiego oka. Niegdyś używane (zwłaszcza w aparatach rentgenowskich) naświetlanie zwykłych błon fotograficznych wymagało w praktyce stosowania tak wysokich dawek promieniowania jonizującego, że jego dalsze stosowanie w dobie dzisiejszej techniki byłoby nieakceptowalne. Bardziej wydajnym sposobem jest wielostopniowe przetwarzanie kwantu promieniowania elektromagnetycznego na impuls elektryczny o odpowiedniej wielkości.
POWRÓT do początku podstronyFoton promieniowania elektromagnetycznego musi najpierw zostać pochłonięty przez substancję zawartą w detektorze. Im wyższa gęstość oraz liczba atomowa tej substancji, tym wyższe prawdopodobieństwo wystąpienia takiego oddziaływania. Pochłonięciu towarzyszy jonizacja, czyli wytworzenie pary jonów. Wprawdzie para ta stanowi już prąd elektryczny, jednak jego natężenie jest o kilka rzędów wielkości zbyt małe, aby mogło zostać zarejestrowane. Dlatego w praktyce stosuje się najczęściej tak zwane "kryształy scyntylacyjne" - czyli takie substancje, które po pochłonięciu kwantu promieniowania jonizującego wytwarzają wiele kwantów promieniowania świetlnego (czyli również elektromagnetycznego, ale o niższej energii). Te z kolei kwanty światła są kierowane na katodę lampy próżniowej. Z katody każdy kwant "wybija" elektrony.
Ponieważ tak powstały prąd ma nadal natężenie zbyt niskie, aby można go było zarejestrować, musi zostać dalej wzmocniony. W tym celu powstały strumień elektronów jest przyspieszany w polu elektrycznym o napięciu rzędu stu-kilkuset woltów na kolejną elektrodę, tak zwaną "dynodę". Każdy z przyspieszonych elektronów, uderzając
Aby możliwe było utworzenie obrazu z zarejestrowanego promieniowania, fotony muszą być zapisywane w sposób uporządkowany. Innymi słowy, musimy dysponować czymś analogicznym do soczewki, która w tradycyjnej fotografii nadaje odpowiedni, "uporządkowany", kierunek padającym kwantom światła. Rolę takowej soczewki w przypadku promieniowania o wysokiej energii pełni kolimator. Sprawia on, że do detektora docierają tylko i wyłącznie fotony padające na niego pod kątem prostym. Zbudowany jest, w uproszczeniu, z ułożonych równolegle rurek ołowianych.
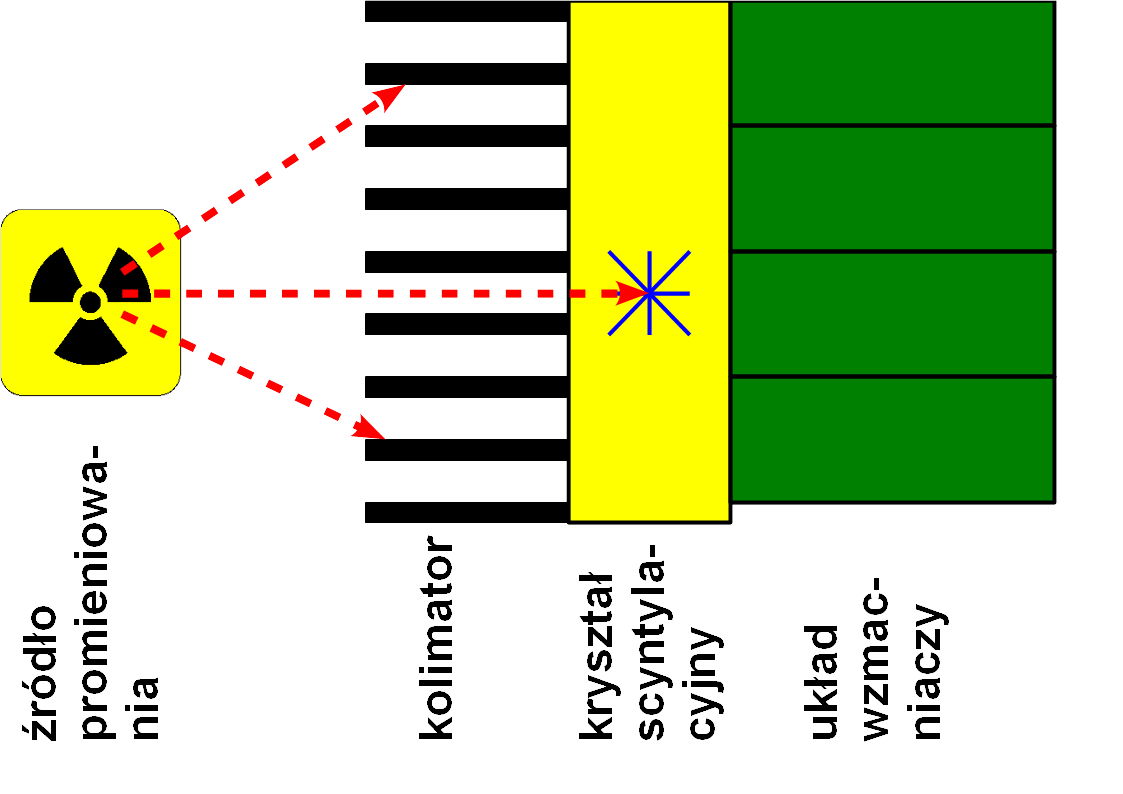
Schemat budowy i działania gamma-kamery. Promieniowanie ze źródła promieniotwórczego biegnące równolegle do przegród kolimatora zostaje przezeń przepuszczone i dochodzi do kryształu scyntylacyjnego (najczęściej jest to jodek sodu domieszkowany talem - NaI/Tl), gdzie zostaje pochłonięte (z wytworzeniem światła) i potem wzmocnione. Promieniowanie o innym kierunku zostaje zatrzymane przez kolimator.
Gamma-kamera umożliwia więc "fotografowanie" pacjenta, rejestrując (zamiast zwykłego światła) promieniowanie wysyłane przez obecne w jego organizmie atomy promieniotwórcze. W zależności od konfiguracji oprogramowania oraz zastosowanego radiofarmaceutyku można za jej pomocą wykonywać obrazy scyntygraficzne statyczne i dynamiczne (rejestracja w dłuższym okresie czasu) - zawsze jednak planarne (czyli dwuwymiarowe, a
Słowo "tomografia" pochodzi od greckiego "tomé" (τομη), które oznacza "przekrój". W skrócie jest to technika umożliwiająca nieinwazyjne uzyskiwanie obrazów przestrzennych (a także dowolnych przekrojów) badanego obiektu lub pacjenta. Termin "SPECT" jest akronimem z języka angielskiego "Single Photon Emission Computed Tomography", co można przetłumaczyć jako "(komputerowa) tomografia emisyjna pojedynczego fotonu". Różnica pomiędzy SPECT, a "zwykłą" tomografią rentgenowską (CT - "Computed Tomography", w Polsce znaną też jako TK lub KT) polega na tym, że w CT wykorzystuje się promieniowanie emitowane przez lampę rentgenowską umieszczoną poza ciałem pacjenta - jest to więc tomografia transmisyjna. W tomografii emisyjnej wykorzystujemy promieniowanie wysyłane przez pacjenta (źródło promieniowania znajduje się wewnątrz ciała badanego). W SPECT rejestruje się niezależnie każdy pojedynczy foton (w odróżnieniu od PET - patrz dalej).
Tworzenie obrazów przestrzennych (a po odpowiedniej obróbce - także obrazów dowolnego przekroju) jest dość złożoną operacją matematyczną, przeprowadzaną przez komputery ze specjalnym oprogramowaniem. Niezależnie
Do dobrej rekonstrukcji obrazów SPECT potrzebne są "mapy atenuacji" badanego obiektu (pacjenta) - czyli mapy pokazujące, w jakim obszarze ciała jak bardzo pochłaniane jest (czyli osłabiane) promieniowanie jonizujące. Mapa taka może być sporządzona przez aparat CT - w istocie obraz CT jest takową "mapą atenuacji". Stąd przewaga SPECT/CT, czyli aparatu hybrydowego, nad SPECT, polega nie tylko na możliwości połączenia dwóch różnych rodzajów obrazów, ale także dokładniejszej obróbki samego obrazu scyntygraficznego.
POWRÓT do początku podstronyCelem dokładnego zrozumienia działania aparatu PET konieczne jest wcześniejsze zaznajomienie się z mechanizmem rozpadu promieniotwórczego β+ oraz oddziaływaniem pozyton-negaton.
Słowo PET jest akronimem z języka angielskiego "Positron Emission Tomography", co można przetłumaczyć jako "pozytonowa tomografia emisyjna". Detektory PET są "niepełnymi", bo pozbawionymi typowych kolimatorów, gamma-kamerami. Istota ich działania polega na równoczesnym rejestrowaniu obu powstających podczas anihilacji fotonów γ (zarejestrowaniu koincydencji). Wiadomo, że źródło tych fotonów (a więc atom emitujący promieniowanie β+) znajduje się w pobliżu linii prostej przeprowadzonej pomiędzy miejscami wykrycia tych fotonów. Po przeanalizowaniu przez komputer wielu milionów koincydencji możliwe jest stworzenie przestrzennego obrazu rozmieszczenia nuklidu w badanym obiekcie (pacjencie). Podobnie, jak w przypadku SPECT, obrazy PET mają lepszą jakość, jeżeli są połączone z obrazami CT (PET/CT).
Obrazy PET (PET/CT) mają generalnie wyższą jakość, niż SPECT (SPECT/CT). Wadą PET-a jest wysoka cena - nie tyle samego skanera, co aparatury potrzebnej do jego funkcjonowania (żeby wspomnieć tylko o cyklotronie do wytwarzania krótkożyciowych β+-radionuklidów oraz o całej radiochemii potrzebnej do syntezy radiofarmaceutyków...).
POWRÓT do początku podstrony
Używany w diagnostyce nuklid Tc-99m (oznaczany też jako 99mTc) pozyskiwany jest w miejscu jego używania z generatora molibdenowo-technetowego, zawierającego izotop molibdenu: 99Mo. Molibden-99 uzyskiwany jest w reaktorze atomowym: albo poprzez rozszczepienie jąder uranu (lub plutonu) i potem wydzielenie tego nuklidu z mieszanki produktów tej reakcji, albo poprzez napromienienie tarcz molibdenu-98 wiązką neutronów. Molibden-99 charakteryzuje się czasem połowicznego zaniku 65,98 godzin (czyli wystarczy dostarczyć jeden-dwa takie generatory na tydzień), poprzez rozpad β- przekształca się w ok. 87,5 % w Tc-99m, reszta
Technet-99m (od słowa "metastabilny") cechuje się czasem połowicznego zaniku wynoszącym 6,01 godzin. Poprzez przejście izomeryczne z emisją kwantu γ (o energii 140 keV) przekształca się
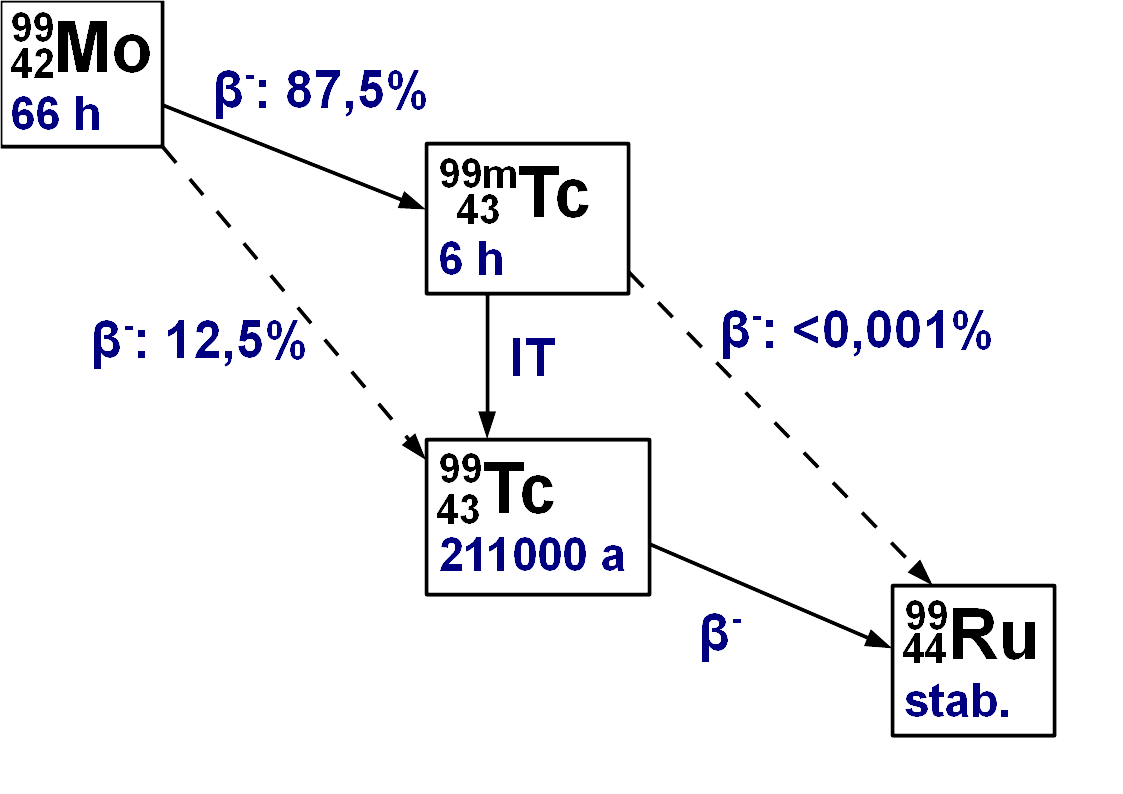
Schemat rozpadu promieniotwórczego molibden-99 - technet-99m - technet-99 - ruten-99
Odpowiedni czas połowicznego zaniku Tc-99m, brak emisji promieniowania korpuskularnego oraz odpowiednia energia kwantu γ, a także łatwość w jego pozyskiwaniu na miejscu użycia, spowodowały, że nuklid ten zaskarbił sobie trwałe miejsce w diagnostyce medycznej.
Technet z generatora molibdenowo-technetowego wypłukiwany jest w postaci nadtechnetanu sodu (nadtechnecjanu sodu - NaTcO4) zawierającego ten metal na +7. stopniu utleniania. Roztwór nadtechnecjanu jest używany do dalszych obróbek chemicznych prowadzących do produkcji wielu radiofarmaceutyków.
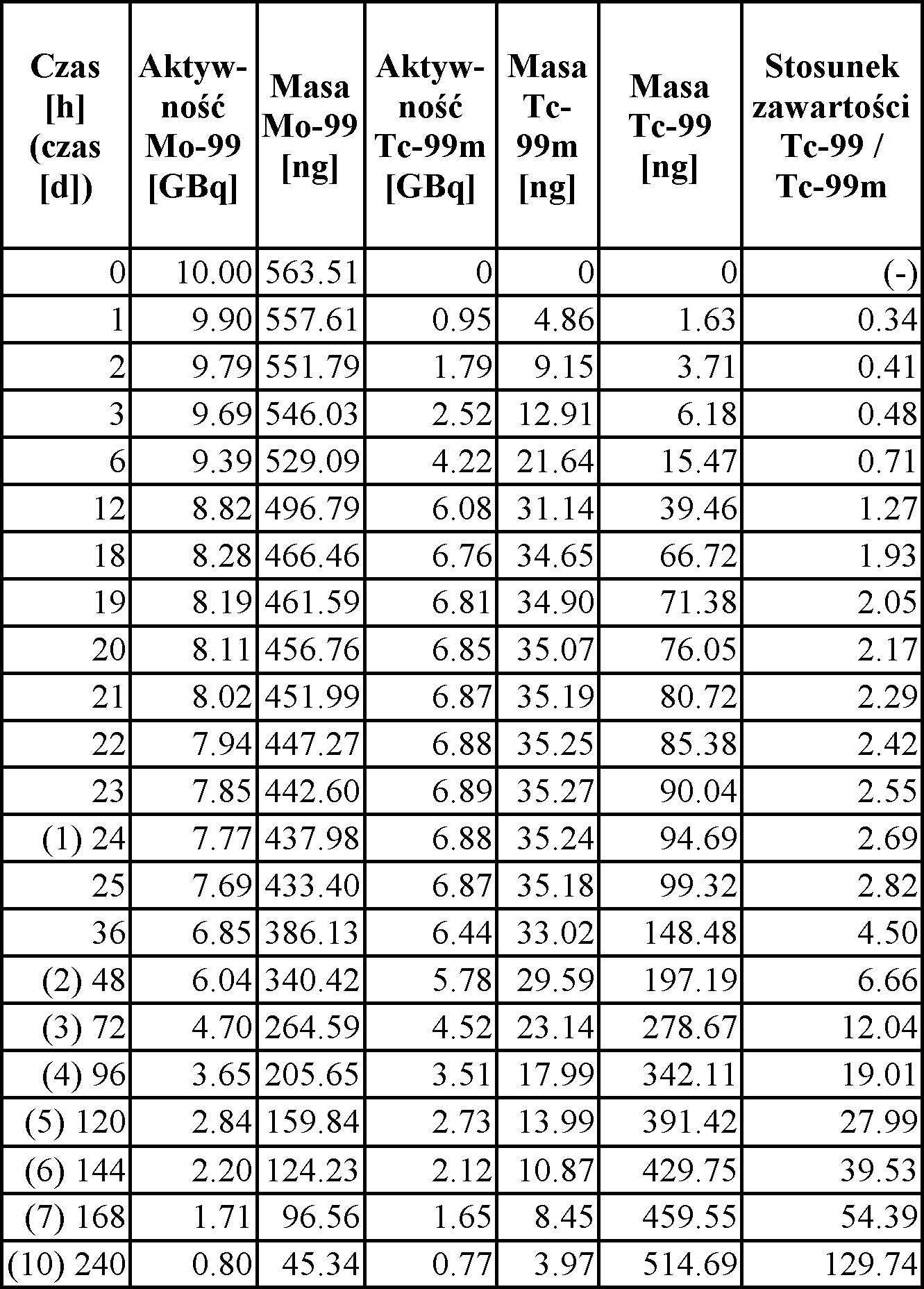
Więcej na temat ogólnych problemów pracy z generatorami tego typu można przeczytać tutaj. W poniższej tabeli przedstawiono zawartość poszczególnych nuklidów w generatorze w funkcji czasu. Zarówno użyteczny dla nas Tc-99m, jak i produkt jego rozpadu - Tc-99 (tak zwany "zimny technet") - znajdują się w roztworze w postaci nadtechnetanu (a więc są identyczne chemicznie). Maksimum aktywności Tc-99m przypada ok. 22,9 godzin po ostatniej elucji (czyli przepłukaniu - usunięciu technetu) generatora. W praktyce szczególnie ważne jest, aby odpowiednio często dokonywać elucji, albowiem obecny w dużych ilościach Tc-99 chemicznie konkuruje z Tc-99m, co może pogarszać jakość otrzymanych radioznaczników, a przez to również jakość uzyskanych obrazów scyntygraficznych. Po upływie 10 dni od ostatniego płukania przewaga zawartości Tc-99 nad Tc-99m jest, jak widzimy, ponad stukrotna, co uniemożliwia prawidłowe przygotowanie praktycznie jakiegokolwiek radioznacznika - nawet jeżeli teoretycznie aktywność pozostającego jeszcze Tc-99m byłaby wystarczająca. Między innymi z tego względu elucji dokonuje się codziennie.
 |
|
Założenie: - generator o aktywności 10 GBq (w momencie ostatniej elucji) zawiera początkowo 563,5 ng Objaśnienia: W kolumnie 1. - czas, jaki upłynął od tego momentu, w kolumnach 2. i 3. - aktywność (A) i masa (M) Mo-99 w danym czasie, w kolumnach 4. i 5. - aktywność (A) i masa (M) Tc-99m w danym czasie, w kolumnie 6. - masa Tc-99, w ostatniej kolumnie - stosunek masy Tc-99 do masy Tc-99m. |
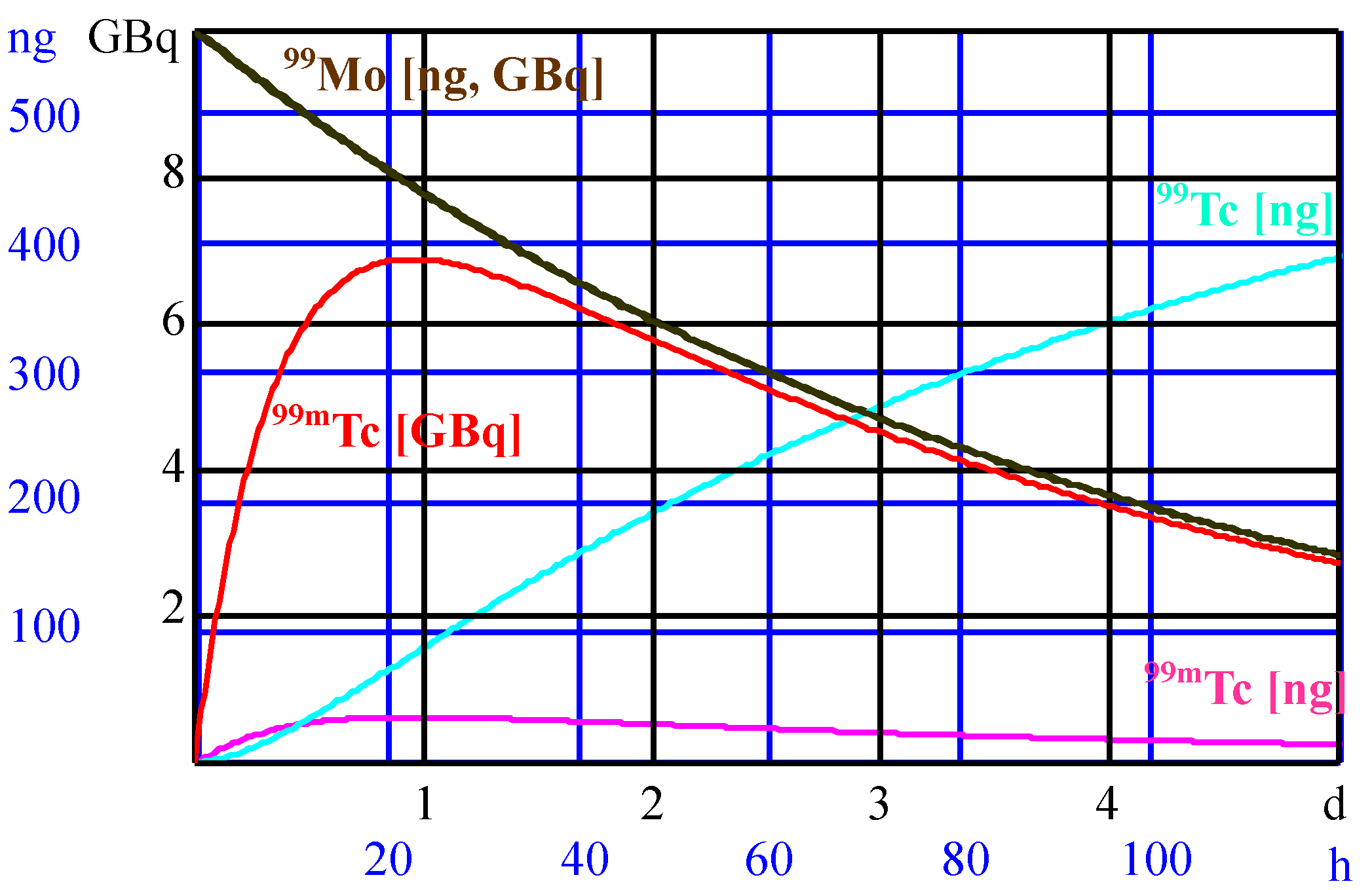
Generator molibdenowo-technetowy o aktywności początkowej 10 GBq, wykres ilości nuklidów (oś pionowa: GBq i ng) w funkcji czasu (oś pozioma: dni i godziny); kolor oliwkowo-brązowy: aktywność i masa Mo-99 (GBq i ng), kolor czerwony: aktywność Tc-99m (GBq), kolor różowy: masa Tc-99m (ng), kolor turkusowy: masa Tc-99 (ng);
Generator molibdenowo-technetowy z zewnątrz
Jeden z promieniotwórczych izotopów jodu - 131I - jest produkowany do celów medycznych w reaktorze atomowym. Są dwa sposoby jego wytwarzania: albo poprzez rozszczepienie jąder uranu (względnie plutonu) i następnie izolację jodu spośród wielu produktów tego rozszczepienia, albo poprzez napromienienie neutronami tarcz telluru-130 (powstający 131Te poprzez rozpad β z półokresem rozpadu ok. 25 minut przekształca się w 131I). Z jodu-131 formowane są następnie kapsułki lub, w zależności od potrzeb, roztwory do wstrzykiwań - w podobny sposób, jak
Jod-131 jest nuklidem o czasie połowicznego zaniku 8,02 dnia. Poprzez rozpad β- przekształca się w ksenon-131 (jeden z gazów szlachetnych). Zasięg tej cząstki beta w tkankach człowieka wynosi około 0,5 milimetra (średnio; maksymalnie do ok. 2 mm).
Jądro atomu jodu-131 wysyła również kwanty promieniowania γ. Powoduje to, że narządy położone daleko
Jod-131 wzbudził duże kontrowersje po awarii reaktora atomowego w Czarnobylu. Ze względu na to, że minęło dopiero nieco ponad 30 lat od tej tragedii, nie można jeszcze definitywnie powiedzieć, czy uwolniony wówczas jod promieniotwórczy rzeczywiście zwiększył zachorowalność na nowotwory tarczycy. Jod ten stosowany jest w medycynie od znacznie dłuższego czasu (od lat czterdziestych XX wieku). Pacjenci objęci są obserwacją. Jak dotąd nie wykazano, aby byli oni bardziej narażeni na nowotwory, niż ogólna populacja (ludzie nie objęci leczeniem z zastosowaniem tej substancji).
Osłony do przechowywania i transportu kapsułek z jodem radioaktywnym
Obecnie znanych jest ponad 3000 różnych nuklidów, z czego ok. 250 jest trwałych (nie podlega rozpadowi promieniotwórczemu). Naturalnie na Ziemi zaobserwowano ok. 340 nuklidów, reszta została otrzymana sztucznie. W medycynie nuklearnej zastosowanie znalazło kilkadziesiąt spośród znanych nuklidów - głównie syntetycznych.
A - liczba masowa T(1/2) - fizyczny czas połowicznego zaniku rozpad - rodzaj rozpadu i współczynnik podziału energia - podano energie najważniejszych rodzajów rozpadu w keV oraz ich udziały procentowe; dla rozpadu β- podano energię maksymalną (end-energy) mean-β - średnia energia cząstek β - do celów wyliczeń dozymetrycznych CE - elektrony konwersji Aug. - elektrony Augera ε - wychwyt elektronu Dane procentowe energii w nawiasach: dane dokładne - udział danej energii dane "do ..." - energie w podanym przedziale mają udziały do ... dane "ok. ..." - energie w podanym przedziale mają sumaryczny udział ... |